福西です。
今このクラスでは、ユークリッドの『原論』第3巻の命題を証明しています。先週と今週で、命題3-10、14、16、20を証明しました。
(以下の命題の日本語(訳)は『ユークリッド原論』(中村幸四郎他/訳解説、共立出版)から拝借しています)
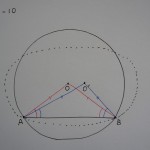
命題3-10 「円は円と二つより多くの点で交わらない。」
R君は、背理法で証明しました。
もし円が円と二つより多くの点で交わったとすると、上の図のような場合が考えられる。
ところで、二つの円が、交わるか接するかした場合に「共通の中心を持たない」ことは、すでに命題3-5と3-6で証明済み。
よって、それぞれの円の中心O、O’は距離を持つはずである。(図)
OA=OB(円Oの半径)、O’A=O’B(円O’の半径)より、それぞれ二等辺三角形が作れ、
∠OAB=∠OBA、・・・(1)
∠O’AB=∠O’BA。・・・(2)
図より、
∠OAB<∠O’AB、・・・(3)
∠OBA>∠O’BA。・・・(4)
しかし、(1)(3)(4)が成り立つなら、
∠O’BA<∠OBA=∠OAB<∠O’AB
となり、すなわち
∠O’BA<∠O’AB
でなければならない。しかし、これは(2)と矛盾。
その原因は最初の仮定にあった。
よって、「円は円と二つより多くの点で交わらない。」(Q.E.D.)
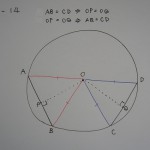
命題3-14 「円において等しい弦は中心から等距離にあり、中心から等距離にある弦はまた互いに等しい。」
これも結局は、
1)円を描いたらすぐ「中心」も描く!
2)円といえば二等辺三角形!(半径が等しい)
この二つがポイントです。R君にはそれを毎度、ワンパターンのように身に染み込ませてもらっていることになります。
そして、ひさびさに三角形の合同条件を使いました。
命題は、図の記号を使うと、
AB=BC⇔OP=OQ
という内容になります。
これを、AB=BC→OP=OQと、AB=BC←OP=OQに分けて証明しました。
どちらも「三辺合同」が鍵ですが、二つ目は三平方の定理(1-47)を使うと楽でした。
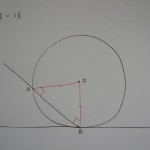
命題3-16 「円の直径にその端から直角にひかれた直線は円の外部に落ちるであろう。(以下略)」
これも背理法で示しました。そして「円と言えば中心」を描き、その「半径を補助線」に描いて、二等辺三角形を作ります。そうすればもう「勝ち」です。
証明の流れは、
「仮に命題が成り立たないとしよう。そうすると、図のような三角形が描けてしまう。これは矛盾。だから命題は成り立つ」
ということです。
命題が成り立たないとすると、図のように∠OAB=90°となります。
すると、△OABは二等辺三角形なので、底角が等しいため、∠OBA=∠OAB=90°
となってしまいます。
すると、180°以上の内角を持つ三角形が描けてしまいました。
これは矛盾です。
よって、命題は成り立つ、ということです。
命題3-20 「円において角が同じ弦を底辺とするとき、中心角は円周角の2倍である。」
これは学校で教わったところの、おなじみの「円周角の定理」(の一つ)です。
見かけ倒しで、実は背理法を使って証明した先の定理たちよりも、こちらの方が計算で証明できるので、簡単だと思います。
これも、「円と言えば中心」を描き、その「半径を補助線」に描いて、二等辺三角形を作ります。
図で言うと、
∠AOB=2∠APB
を証明することになります。
まず、図のように△OPAと△PPBが二等辺三角形であることに注目します。そしてそれぞれの底角の大きさに、たとえばx、yと代数的な記号をあてる(自分で名づける)ことができるかどうかが、次のポイントです。(この「名づける」という当たり前を当たり前にできることが、とても重要な力です)
それさえできれば、あとは、
∠APB=x+y
∠AOB=2(x+y)
であることが示せます。
次週は、少し難しいと思って後回しにしておいた、命題3-12を証明します。