福西です。
春学期の最後は、次のような問題を考えました。
問い
豆電球が1000個あり、1~1000まで番号が付いている。
そしてその豆電球にはそれぞれスイッチが付いており、1回スイッチを入れるごとにON、OFFが切り替わる。
ONの時は「明るく」なり、OFFの時は「暗く」なる。
最初は全部の豆電球はOFFの状態である。
以下、1の倍数、2の倍数、3の倍数・・・1000の倍数と順に、その番号のついた豆電球のスイッチを入れていく。
果たして、最後の状態では、「明るい」豆電球はいくつあるか?
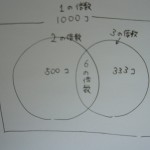
1の倍数で、全部が付く。
2の倍数で、半分が消えます。
さて、3の倍数で・・・というと、どうなるでしょうか。
生徒たちは、3の倍数の個数が、以下のような分数による計算で求められることに気づきました。
1000÷3≒333個(切り捨て)
ここで、小数で出さないのがミソです。
同様に振り返ると、
1の倍数は、1000÷1=1000個
2の倍数は、1000÷2=500個
と、いずれも分数(と切り捨て)で統一的に計算できることが見て取れます。
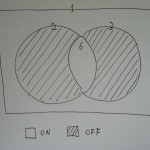
図にかくと、こんな感じになります。
問題は、6の倍数のところがダブっていることです。
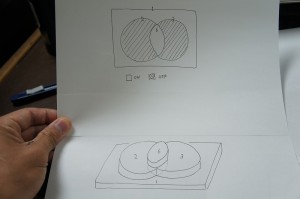
立体的にかくと、こんな感じです。
2の倍数と3の倍数を単純に足すと、足しすぎているところが生じます。それが6の倍数の部分です。
そこで、6の倍数の個数を計算する必要が出てきました。
1000÷6≒166(切り捨て)
これにより、「2の倍数」または「3の倍数」である個数は、
1000/2+1000/3-1000/6=500+333-166=667個(ただし各分数は切り捨て)(注)
と求まります。
(注)小学生は「ガウスの整数」の記号をまだ習っていないので、このような言い表し方をしています。
そして、それを全体から引いて、
1000-667=333個
が、「2の倍数」でも「3の倍数」でもない個数となります。
しかし、これでやれやれと思いきや、よく考えたら、問題の意図は、「明るい豆電球の個数はいくらか?」なので、これではまだ答になっていません。
6の倍数のところは、実際には「明るい」ので、これは足さなくてはいけません。よって、
333+166=499個
が「3の倍数までスイッチを入れた」時の状態となります。
あれ?
よく見ると、500個(2の倍数のスイッチを入れた時)から、1個しか減っていませんね。
ムムム、これは不思議!
しかし途中の計算で、考え違いは見当たりません。式に直すと、
1000-1000/2-1000/3+1000/6+1000/6(ただし各分数は切り捨て)
となります。
ここでぱっと見て気付くことは、1000/6を2回足していることです。これはややこしいですね。こんなので法則性が見つかるのでしょうか・・・?
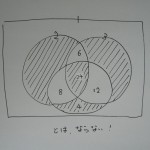
さて、次は、4の倍数のスイッチを入れてみます。
すると・・・
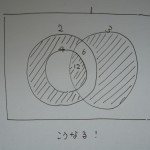
と、左の図のようにきれいになるかと思いきや、右のような形となってしまいます。これではどこを足して、どこを引いたらいいのか、早くもこんがらがってしまいました。次に5の倍数、6の倍数・・・となると、もうお手上げです。
分数による計算は、こうやって頓挫してしまいました。
そこで、今度は別のあたりを付けるために、問題を単純にしてみました。
豆電球が1000個だから大変なのであって、10個にして考えてみれば、何か見通しがつくのでは?と考えたわけです。
(つづく)