
福西です。
この日は、A君は、以前証明した「三角不等式」(『原論』1.20)のつながりで、その拡張と、またシュワルツの不等式を証明しました。そこで、方程式と幾何とのつながりを見、また学校で最近していた「論理」に使う不等式に慣れてもらいました。
三角不等式
|x+y|≦|x|+|y|
(これは、『原論』1.20の「すべての三角形においてどの2辺を取ってもそのその和は残りの1辺よりも大きい」という命題に当たります)
三角不等式の拡張
|x+y+z|≦|x|+|y|+|z|
A君の証明
以前証明した|x+y|≦|x|+|y|を使い、
|x+y|≦|x|+|y|
|y+z|≦|y|+|z|
|z+x|≦|z|+|x|
を辺々足し合わせる。
|x+y|+|y+z|+|z+x|≦2(|x|+|y|+|z|)
(|x+y|+|y+z|+|z+x|)/2≦|x|+|y|+|z|…(1)
また、
(x+y)+(y+z)+(z+x)≦|x+y|+|y+z|+|z+x|
より、
2(x+y+z)≦|x+y|+|y+z|+|z+x|…(2)
そして両辺の絶対値を取ると、(*注)
2|x+y+z|≦||x+y|+|y+z|+|z+x||=|x+y|+|y+z|+|z+x|…(3)
よって、(1)式は、
2|x+y+z|/2=|x+y+z|≦|x|+|y|+|z|
となり、題意が示せた。
A君のアイデアは、対称性を利用して、等価な「解きやすい形」に変換するという点です。他にも色々と証明の仕方はあるとは思いますが、今回の自分の「たどった道」をぜひ自信の一つにしてください。
(*注)
授業ではうっかり「大丈夫」と言ってしまったのですが、実はx+y+zが負の場合があり、そうなると(2)式の両辺で正負が異なって、絶対値を取った時に(3)式の不等号の向きが変わってしまう可能性があります。
(たとえば-100<1ですが、両辺の絶対値を取ると、100>1となり、このように不等号の向きは一般には保存されません)
その考察が抜けてしまっていましたので、追記します。
・x+y+z≧0の場合
(2)から(3)式の導出は自明。
・x+y+z<0の場合
もし2|x+y+z|≦|x+y|+|y+z|+|z+x|が成り立たないと仮定すると、2|x+y+z|>|x+y|+|y+z|+|z+x|となる。すると、
2|x+y+z|
>|x+y|+|y+z|+|z+x| ←この不等号に等号が入っていないことに注意
≧|x+y+y+z|+|z+x|
≧|x+y+y+z+x|
=2|x+y+z|
すなわち、
2|x+y+z|>2|x+y+z|
2>2
となり、矛盾。
よって仮定が間違っていることが示せたので、x+y+z<0の場合でも、2|x+y+z|≦|x+y|+|y+z|+|z+x|は成り立つ。
[お詫び]
両辺の正負を考えずに絶対値を取るというのは、危険でした。すみません、A君。
さて、A君が証明してくれたのは、3つの項の三角不等式でしたが、それを4つに増やした、
|x+y+z+w|≦|x|+|y|+|z|+|w|
でも、できることを考察しました。
ここで、A=x+y+zとおくと、|x+y+z+w|は|A+w|と表せるので、普通の三角不等式が使えます。そのことを示唆し、A君には、
|A+w|≦|A|+|w|≦|x|+|y|+|z|+|w|
(2つ目の不等式は|x+y+z|≦|x|+|y|+|z|によります)
となって、以下、2項の三角不等式を繰り返していけば、一般の拡張|x1+x2+…xn|≦|x1|+|x2|+…+|xn|についても示せるということを確認してもらいました。
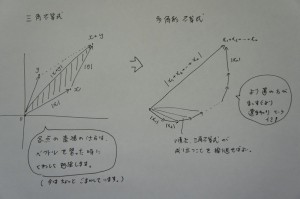
そしてこのような拡張は、幾何学的には三角形から多角形への拡張だと解釈できます。
(三角不等式|x+y|≦|x|+|y|とその拡張。いずれも、「寄り道無し」≦「寄り道あり」を表しています)
三角不等式は、絶対値と並んで、一見理屈が単純すぎて、「つい分かった気になってしまう」のに「なぜか苦手」なものの代表格だと思います。(一方、三平方の定理が得意だというのは、演習問題で何度も解いているからです)。けれども実際、三角不等式も、三平方の定理と並んで、とても重要な関係式です。(*)それが幾何学的な「三角形」と関係があるということで、いろんなところで「目に付く」ことをお勧めします。
(*)等式よりもむしろ不等式の方が主役を張る分野が数学にはあって、たとえばベクトルxとy、また関数f(x)とg(x)の「近さ」をはかりたかったり、それに関係する証明をしたい時には、この三角不等式が再び活躍を見せます。
次にシュワルツの不等式(の項が2つの場合)も証明しましたが、長くなったので次の記事に分けます。
山下です。飛び入り参加したいクラスの1つです。