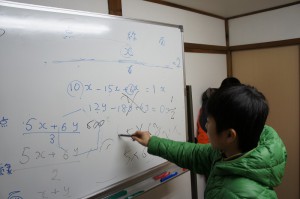福西です。
ブログには書いてませんが、前回、平面や球面(またそれらの穴あきの場合)の三角形分割を実験し、帰納的に「オイラーの多面体定理」を導きました。
オイラーの多面体定理は、(穴のあいていない)球面の場合では、
点の数-線の数+面の数=2
という関係を与えます。
今回はその結果を利用して、「5種類の正多角形(プラトン立体)」を作りました。
正多面体とは、正多角形で作れる立体のことです。
また正多角形とは、等しい長さの辺で作れる多角形のことです。
そして、そのような正多角形で作れる正多面体は、実は3次元では5種類しかないことが知られています。
(小学生クラスでは証明は省きましたが、オイラーの多面体定理と文字式を使えば簡単に証明できます)
また正多面体を構成できる正多角形は、1点の周りに貼り合せる多角形の角の合計が180度より大きくかつ360度未満でなければならない(180度以下では貼り合せができず、360度以上だと平面から立体に起き上がれない)という制約から、正3角形、正方形(正4角形)、正5角形の3種類しかありません。
すなわち、以下のような場合のみとなります:
1)正3角形で作る場合
1点のまわりに集まる正3角形(1つの角=60度)が
i)3つ
ii)4つ
iii)5つ、
(6つは360度なのでアウト)
2)正方形で作る場合
1点のまわりに集まる正方形(1つの角=90度)が
iv)3つ、
(4つは360度なのでアウト)
3)正5角形で作る場合
1点のまわりに集まる正5角形(1つの角=108度)が
v)3つ。
そして、
i)→正4面体、ii)→正8面体、iii)→正20面体、iv)→正6面体、v)→正12面体
となります。
【補足】
授業ではサイコロの視察により、証明は省きましたが、たとえば上の3)のv)の場合だと、以下のようにします。(興味のある方は実際に計算して調べてみてください)
1)正5角形(面)の数=n
2)正5角形n枚の点すべて=5n
3)多面体を作った時の実際の点の数=5n/3(1点のまわりに正5角形が3つ集まるので、1点を3重に数えていることになるので)
4)正5角形n枚の線すべて=5n
5)多面体を作った時の実際の点の数=5n/2(辺を2重に数えているので)
6)これらの結果をオイラーの多面体定理に代入すると、
5n/3-5n/2+n=2。
これを解いて、
n=12。
他のi)~iv)についても、同様に計算すれば、n=4、8、20、6が出てきます。
さて、今回は「ひねもす」を使って上の5種類の正多面体を実際に構成してみました。
「ひねもす」では、点にはジョイントを、線にはちいもすを使って表現しました。問題はそれらが「いくつずつ必要か?」ということですが、簡単な視察とオイラーの多面体定理による計算から導き出すことができます。(もちろん、上の例で挙げた計算式の中でも求められます)
点の数と線の数のどちらが数えるのが難しいかということですが、線の数の方がおそらく数えにくいと思います。そこで、点をサイコロの視察から数えた後、オイラーの多面体定理に代入して、線の数(以下のx)を得ました。(ちなみに面の数は「正n面体」のnそのままです。)
(点、線、面の数) (オイラーの多面体定理)
正4面体 (4、6、4) (4-x+4=2 x=6)
正6面体 (8、12、6) (8-x+6=2 x=12)
正8面体 (6、12、8) (6-x+8=2 x=12)
正12面体 (20、30、12) (20-x+12=2 x=30)
正20面体 (12、30、20) (12-x+20=2 x=30)
正多角形の面の数が増えていくからと言って、必ずしも点や線の数も増えるわけではないという結果が、面白いです。
さて、上の5つの立体をすべて1個ずつ作るには、合計ちいもす(線)は90本、ジョイント(点)は50個必要だと分かりました。
そして実際に作ってもらっている様子が、以下の写真です。計算通り、「ぴったり」と部品を使い切って、「おお~!!」となりました。
作った後もそれらを眺めながら、色々と考察に花が咲きました。

最後は「サッカーボールを作りたい!」(「正5角形と正6角形を何枚組み合わせれば多面体が構成できるか?」)という問題を一緒に考える所で終わりました。