
福西です。
この日は、「最短距離問題」を考えました。
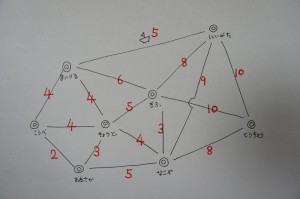
問題:「きょうと」から出発して、地図上の町をすべておとずれ、また「きょうと」にもどってきてください。道の数字は、そこを通った時にかかる時間です。合計時間ができるだけ小さい通り方をさがしてください。
(イメージとしては、お正月におばあちゃんや親せきの家をすべて回って、お年玉をもらいに行くとします。(で、もらったらすぐ帰る(笑))。そしてできるだけ早く自分の家に帰ってくるという設定です)
数字が小さいので簡単そうに見えますが、実はこれだけでものすごく難しい問題です。授業では説明しませんでしたが、一般にA地点からB地点への最短ルートを見つけるという問題であれば、理詰めで、また効率よく解く方法が存在します。
しかし「すべての地点を通って」「スタート地点に戻ってくる」という条件が加わると、これはたちまち、(理詰めで、また効率よく)最適解を見つける方法がなくなってしまうから不思議です。(もしご興味のある方は、「巡回セールスマン問題」で検索してみてください)。
授業では、経験則にのっとって、よりよい答に更新していくという原始的な手法を取りました。それ自体は難しいことはではなく、足し算の練習になります。
最初は「50時間」以上の答から出発して、いろいろな道を試しながら答を見つけていきました。時にいい結果が出たり、期待を裏切られたり、でこぼこしながら、だんだんいい答へと収束していきました。またそうやって見つけたパターンは、結果の良し悪しを問わず、1枚ずつストックしていきました。バリエーションにも意味があります。
ちなみにSちゃんが44時間(43時間だったかもしれません)で、クラスでは一番最善の答を見つけ出していました。
私も自分で作った問題なのでやってみましたが、「40時間」の答を見つけました。(ただしそれが「最適解」であるかどうかは、私には難しい問題で分からりません^^;)。40時間を切ってみよう! あるいは40時間が最適であることの証明をやってみよう! という方はぜひぜひ挑戦してみてください。
問題自体は単純で、生徒たちは「もっと紙ちょうだい」と食いついてくれました。「すぐに飽きてしまうかな・・・?」というこちらの心配はよそに、結局授業時間のほとんどをそれだけで考え続けてくれました。(何度コピーを取りに行ったかしれません^^;)。結局一人10枚ずつぐらい答を作っていました。その知的体力には「すごいなあ!」と目を瞠りました。
<補足> 動的計画法
上で考えたことは、一見「お年玉をもらいに行く」とか、郵便配達といった、具体的な話以外には役に立たなそうですが、抽象化すると、AとBが「似ているか」「そうでないか」ということを考えていることになります(距離が近い=似ている)。それは「パターン認識」という分野で、たとえばデジカメ(や防犯カメラ)で撮った写真の顔認識。また音響や画像の雑音処理。ほかにもパソコンでよく使うデータの圧縮技術など、実は意外なところで、幅広い応用性を持っています。またそれは現代社会で工夫・改良が求められている切実な懸案でもあります。
さて、A地点からB地点への最短ルートを見つけるという問題では、理詰めで最適解を求める方法が存在することを述べましたが、そのことを最後にかいつまんで説明しておこうと思います。(授業では触れませんでしたが、「なぜこんな問題を考えたのか」という背景として書いておきます)
単純化のために、以下のようにします。
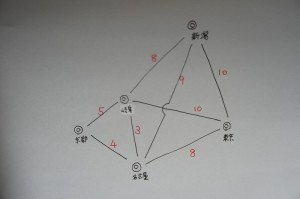
問題:「京都から東京へ行く最短ルートを見つけよ」(数字は所要時間)
これぐらいの規模なら、ぱっと見ただけで「京都→名古屋→東京」が「12時間で最短」だとわかりますが、それが「本当に最短である」と言えるでしょうか。おそらく他の道もすべて試さなければ、それは言えないでしょう。けれども以下の方法では、総当たりによらずに出てきた答が最適であることを保証してくれています。
逆解きで(ゴールから)考えます。
1)東京に行く道は、3つあります。
「新潟→東京」=10
「岐阜→東京」=10
「名古屋→東京」=8
2)そして、新潟から東京に行く道は、3つ考えられます。(その計算で上の1)を使います)
「新潟→東京」=10
「新潟→岐阜」+「岐阜→東京」=8+10=18
「新潟→名古屋」+「名古屋→東京」=9+8=17
下の二つは、当たり前すぎて考える必要がないものですが、念のためです。そして、この三つのうち、一番最短なのは、もちろん寄り道しない「新潟→東京」=10です。
そして、新潟から東京へ行く道を考える時は、必ずこの道をとることにします。
というのも、新潟から東京へ行く際に、迂回するなり他のルートを通った時点で、「全体がもはや最短になる」ことはありえなくなってしまうからです。それもなぜなら、「もし全体が最短ルートになっているなら、その部分部分も最短ルートで構成されている」からです。(これを「最適性の原理」といいます)。
つまり、今は「最短ルートを探している」ので、新潟からあとの「部分」についても結局最短でなければなりません。よって「迂回すればもっと最短になるのでは?」ということは、もはや考えなくても良いことになります。(これ自体はくどくどしい言い方ですけれど^^;)
そこで、
最短(「新潟→東京」)=10
と記憶しておきます。
3)同様に、岐阜→東京、名古屋→東京についても、
最短(「岐阜→東京」)=10
最短(「名古屋→東京」)=8
と記憶しておきます。
4)さて、京都から東京へ行く道を考えます。
ここで、岐阜を通るか、名古屋を通るかで迷いが生じます。ですがミソは、岐阜以降、名古屋以降については、すでに3)で最短ルートが考えられていることです。これを使います。
「京都→岐阜→東京」は、「京都→岐阜」+最短「岐阜→東京」=5+10=15
「京都→名古屋→東京」は、「京都→名古屋」+最短「名古屋→東京」=4+8=12
そしてこれ以外に考える必要はありません。これで最短ルートが見つかりました。
答「京都→名古屋→東京」
せっかく上の2)で新潟についても考えていたので、「新潟は?」と思った人がいるかもしれません。そうなのです。新潟をあえて通る必要がないことは、岐阜を通った時点で、すでに3)で、最短ルートが新潟を通らないことがわかっているからです。(このように「ぐるぐる考えないといけない可能性」から解放されることが嬉しいわけです)
以上、即席なので例があまりよくなくて、ありがたみが薄かったかもしれませんが、こんなふうにして考えると、最短ルート(最適な答)を確実に見つけ出すことができます。(時間があればもう少しいい例を出したいと思います)。
これは「動的計画法」という解き方で、リチャード・ベルマンという人が「最適性原理」(「最短ルートの部分もまた最短であること」)から導き出しました。私自身がこの方法を習った際には、「よく考えられているなあ!」と感動を覚えたのですが、どうでしょうか・・・(^^)。
ただし、この方法でも、「すべての地点を通ってスタートに戻ってくる」という問題になると、うまくいかないのが「ムムム・・・」です(苦笑)。
数学は実に身近なところにあるのですね。
山下先生、コメントありがとうございます。
「抽象」というと、悪いもののように思われがちですが、数学が持つそれには「ほんと、役に立つなあ!」と感じることがしばしばあります。そのおかげで、色々な問題を「同じ」ようにして扱えるわけですから・・・(ただし、何に対して使えるかは、最初分からないわけですけれど・・・^^;)
このクラスでは、いつか「ああ、あれがこれなのか」と生徒たちに思い出してもらえるような、そんな種まきをしていきたいと考えています。
高校で物理を習ったとき、練習問題に「ボールを投げて落ちるまでの時間を求めよ」というような問題があり、数式を解くと答えが二つ出てくることにえらく感動したことを覚えています。一つは何秒後というまともな答え。もう一つは0(ゼロ)という答え。つまり投げる前の手にボールを持っているときの状態だ、と言うことですね。理論と現実がシンクロし、おお!と思いました(笑)。
山下先生、コメントをありがとうございました。福西です。
>理論と現実のシンクロ
数式の「意味」が見えると、「おお、こいつ(数式)って、ただ黙っているようだけど、偉いなあ!」と思わず呟いてしまいますね(^^)。
学校で習う教科はもうお膳立てされていますが、それをただ黒板の前で受け身に感じているのでは損だということなのでしょうね。
「おお!」とひとりで感動したり、血が通っているように感じることが大切だなあと私も思います。(私自身はそれを、浪人した時の復習や、大学に入って体系化するようになってから、ようやく感じました)。
そう言えば岸本先生が、英語クラスの記事で「教科でも問題でもなく、英語とは何かということを考えてほしい」と書いておられたのを連想しましたが、これもいわばシンクロですね(笑)
私も思い出しついでに、その数式にあらわしてみますと、ボールの速度を
v=v’-gt
とした時、それが地面(y=0)に帰ってくる時刻は、積分すると、
y=v’t-(1/2)gt^2
となり(ここで2乗が出てくることがミソですね)、これをy=0について解けばよいので、
t(v’-gt/2)=0。
すなわち、
t=0
t=2v’/g
というわけですね。
因数分解してかっこでくくった時、かっこの前に「ちょこん」といるtが、「おお! こやつ、ちゃんと意味があってここにいるぞ!」と思えることは、物理でもあり、数学でもあり、それでいて国語(物語の力)なのかなあとも思います。(何よりも国語・・・。)