
福西です。冬学期の授業を思い出しながら書いています。
この日(2/20)は、以下の問題を1時間考え続けました。
問い:「正100角形の対角線の本数はいくらか?」
(Ka君の計算用紙)
さっそく手を動かして、3角形から考えていきました。
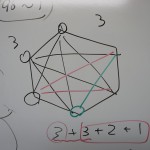
左は6角形で考察しているところ。右は8角形。
6角形は、3+3+2+1=9本、
7角形は、4+4+3+2+1=14本、
8角形は、5+5+4+3+2+1=20本、と分かりました。
最初は、数えもれや、数えすぎに試行錯誤が見られましたが、注意しながら引いていると、じきに、「ムダなく、ムラなく」数え上げる方法が見つかりました。
「これって(頂点が隣に移るごとに)、対角線が1本ずつ減っていってないか?」
と気づいてくれたからです。それがまず、最初の手ごたえでした。その時の二人の顔が、まるで強敵の「弱点」を見つけたかのように、「ニヤリ」としたのが印象的でした。
そのあと、角を1つ(あるいは2つ)ずつ増やしていって「あたり」を付けて考えていくことで、じきに法則性そのものが見えてきました。
「そうか! 6角形やったら、3+3+2+1になる。だって、最初の『3』というのは、6角形の『6』から3を引いた数なんや」と生徒。
「その『3』というのは、どっから出てきたん?」と私。
「だって、対角線は、6つ点があるうちの、自分と、その両隣の点を除いた点に引けるから。つまり、自分とその両隣というのが、『3』で、それを引いた数が、最初の点から引ける対角線の本数になる」と生徒。
なるほどです。そのように、自分で理屈を説明するところに嬉々としてくれる様子が、実に頼もしいなと感じました。
ここで私からは、「3+3+2+1」や「4+4+3+2+1」となるのは分かったけど、最初だけ、3+3+・・・、4+4・・・と、同じ数を2回数えるのが不思議だなあ、と付け加えました。それは(私も含めて)クラスみんなの不思議でした。
対角線の数
3角形 0 (対角線は引けないので、0本になります)
4角形 2 (おなじみの「ばってん」の形で2本になります)
5角形 5 (注:対角線は3本ではなく、「星」の形で5本になります)
6角形 9
7角形 14
8角形 20 (このあたりから、対角線を引くコツがわかってきました)
9角形 27 (このあたりから、俄然、ある規則性、法則性が見えてきました)
・・・
このように、いきなり100角形で考え出さずに、単純なところから攻めていったのが、ミソだなと思います。難しいときは単純なところから考える。あるいは極端な例で考える。この考え「方」自体は、問題が変わっても通用する方法です。だんだんとそうした「パターン」に慣れてきたことを感じました。
(その2に続きます)













“かず5年(0220)その1” への1件のフィードバック