
福西です。
先週、高校生のA君が(2×2の)行列の固有値を求める公式を作ってきたと報告してくれました。(以下代筆です)

ちなみにa+d=tr(A)(トレース)、ad-bc=det(A)(行列式)と表すこともできます。
そして次の週には、行列のn乗を求める公式まで作ってきました。すごい発展だと思います。
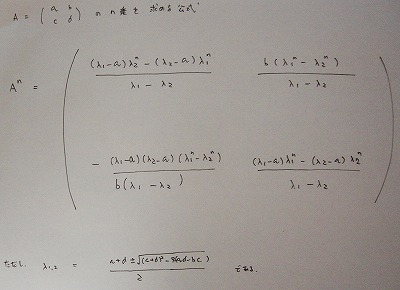
一番下の「ただし」のところに、前回の結果が使われています。
この公式では、λ1≠λ2、b≠0を暗に仮定しています。b≠0の条件を外して書き直すとすれば、
(i) Aが対角行列すなわち
A=[a 0]
[0 d] の場合は、
A^n=[a^n 0 ]
[0 d^n]
(ii) Aが対角行列でなく、b≠0の場合は、
(A君が求めた)上記の公式
(iii) Aが対角行列でなく、b=0の場合は、
Aを転置させ、A’=[a d]
[b c]
について、(ii)の公式を適用すると、(A’ )^nが求められる。
((A’ )^nは(A^n)’ なので、非対角成分を逆に見ればA^nが求められる。)
となります。
λ1≠λ2の仮定はまだ外せていませんが、そこを詰めようとすると大学レベルになってしまうので、今は未完成のままでもいいと思います。何にでも公式を作ろうというA君の意欲に感心しました。